Do Christmas Present Decisions based on ILPs

I have a very large family which means that every year for Christmas many persons are forced to buy many presents for other members of my family. Thus, about fifteen years someone within my family had the idea that everybody should not gift a present to anybody else any longer but to only one person each year. 

The idea got adopted and thus, since then, every year, every person in my family has to buy a present for only one person within the whole family. The complicate thing with this solution is that somebody has to decide which person has to buy a present for which person each year. This sounds easy at first, as a simple draw could solve the problem. However, there are some additional constraints that make the process more complicate:

1. First, each person should get exactly one gift.
2. Second, some combinations are excluded. For example, my mother will always buy a present for my father and I will buy a present for my mother as well which should forbid these combinations for the draw.
3. Third, it should be avoided that a person has to buy a present for the same person as in the last year. Ideally, every person should have to buy a present for a person it never gift a present before.

A simple example for a family consisting of six members.

To get this more clearly let us look at an example: Imagine two sisters, both having a husband and each one child. Thus, the family member group consists of two cousins and their parents. A valid combination would be that

• Husband 1 buys a present for Aunt 2
• Aunt 1 buys a present for Child 2
• Child 1 buys a present for Husband 2
• Husband 2 buys a present for Aunt 1
• Aunt 2 buys a present for Child 1
• Child 2 buys a present for Husband 1

The constraints include:

• No present from Husband 1 for Aunt 1
• No present from Husband 1 for Child 1
• No present from Aunt 1 for Child 1
• No present from Aunt 1 for Aunt 2
• …

Somehow someone in my family thought me to be the smartest guy (sorry family folks). And thus, I had to draw all the combinations every year. Originally, I did a simple draw every year and simply changed the drawn combinations until everything worked right by changing combinations for up to two hours until all the constraints were considered in the final result. However, over the years more and more members of my family joined the one-present-per-family-member idea and thus, today the draw includes presents and constraints for sixteen family members, all of them having their personalized constraints!

As last year a colleague of mine showed me integer linear programs (ILPs) [1] and how they could be used to compute optimal solutions for constrained mathematical problems, I had the idea to apply them for my Christmas present problem. And this is what this article is about: how to compute Christmas present combinations with ILPs.

How do ILPs work? Actually they are quite simple. First, we define a set of variables for which we want to compute an optimal solution (e.g., we can say we have to variables a and b for which we want to compute integer values). Second, we define an objective function (e.g., we can say that the sum of a and b should be as small as possible). Third, we can define some constraints (e.g. that a is b-2 and b is 2*a). Afterwards, an ILP solver will compute an optimal solution for our ILP. In our example the optimal solution will be a=2 and b=4.

So how does an ILP solution for our example looks like?

First, we have to define our variables. For each valid combination of persons buying and getting a present, we define a variable that can be either 0 or 1 indicating a non-drawn or drawn combination. Thus, we need the following variables: aunt1_husband2, aunt1_child2, husband1_aunt2, husband1_husband2, husband1_child2, child1_aunt2, child1_husband2, child1_child2, aunt2_husband1, aunt2_child1, husband2_aunt1, husband2_husband1, husband2_child1, child2_aunt1, child2_husband1, child2_child1.

Next, we have to specify our constraints. First, each person has to buy exactly one present: For example, the constraint husband1_aunt2 + husband1_husband2 + husband1_child2 = 1 ensures that husband 1 will buy one present. We specify such a rule for each member of the family. Afterwards, we have to define a similar rule for each family member indicating that it will receive exactly one present. For example, again husband 1: aunt2_husband1 + husband2_husband1 + husband2_child2 = 1.

Following, we have to consider that we want to avoid presents from the former years. Thus, for each drawn person we define a cost function, which we afterwards try to optimize (i.e., minimize) with our ILP. For each family member we define a cost that consists of all former presents this member got before. For example, if husband 1 got two presents from child 2 and one present from aunt 2 before, its cost function will be: cost_husband1 = 2 child2_husband1 + aunt2_husband1.

Finally, we have to specify our objective function which is simply to minimize the cost of former presents: min cost_aunt1 + cost_husband1 + cost_child1 + cost_aunt2 + cost_husband2 + cost_child2.

And we are done. Our whole program looks as shown below (if we consider no former presents):

/* Objective function */

min: cost_Aunt1 + cost_Husband1 + cost_Child1 + cost_Aunt2 + cost_Husband2 + cost_Child2;

/* Constraints */

/* One customer per guy. */

Aunt1_Husband2 + Aunt1_Child2 = 1;

Husband1_Aunt2 + Husband1_Husband2 + Husband1_Child2 = 1;

Child1_Aunt2 + Child1_Husband2 + Child1_Child2 = 1;

Aunt2_Husband1 + Aunt2_Child1 = 1;

Husband2_Aunt1 + Husband2_Husband1 + Husband2_Child1 = 1;

Child2_Aunt1 + Child2_Husband1 + Child2_Child1 = 1;

/* One present per guy. */

Husband2_Aunt1 + Child2_Aunt1 = 1;

Aunt2_Husband1 + Husband2_Husband1 + Child2_Husband1 = 1;

Aunt2_Child1 + Husband2_Child1 + Child2_Child1 = 1;

Husband1_Aunt2 + Child1_Aunt2 = 1;

Aunt1_Husband2 + Husband1_Husband2 + Child1_Husband2 = 1;

Aunt1_Child2 + Husband1_Child2 + Child1_Child2 = 1;

/* Cost per customer. */

cost_Aunt1 = 0;

cost_Husband1 = 0;

cost_Child1 = 0;

cost_Aunt2 = 0;

cost_Husband2 = 0;

cost_Child2 = 0;

Now, we can use an ILP solver to solve the problem. Here, we use the LPSolve IDE that can be obtained from [2]. By solving the ILP the get the following result:

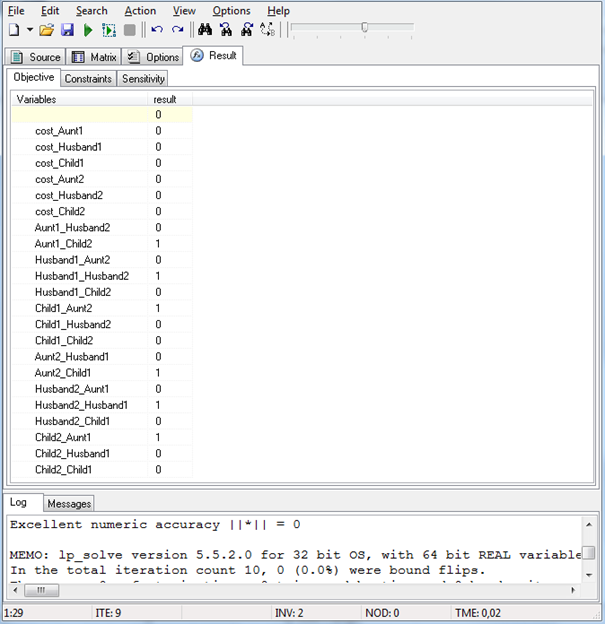ILP solving result.

Thus:

• Aunt1 buys a present for Child2
• Husband1 buys a present for Husband2
• Child1 buys a present for Aunt2
• Aunt1 buys a present for Child1
• Husband2 buys a present for Husband1
• Child2 buys a present for Aunt1

If we want to compute the combinations of the following year, we simple have to add last year’s combinations, by altering the costs to:

/* Cost per customer. */
cost_Aunt1 = Aunt1_Child2;
cost_Husband1 = Husband1_Husband2;
cost_Child1 = Child1_Aunt2;
cost_Aunt2 = Aunt2_Child1;
cost_Husband2 = Husband2_Husband1;
cost_Child2 = Child2_Aunt1;

And we get a new valid and optimal combination.

The attentive reader may have noticed that the number of constraints to be formulated increases squared with every additional family member. Furthermore, I mentioned that our present group currently includes sixteen participants. Formulating such an ILP by hand is both cumbersome and error-prone.

Thus, this year, I implemented a simple DSL using Eclipse and EMFText [3] to formulate the problem in a more elegant way:

Formulation of the present problem in a simple DSL.

The DSL is more or less self-explanatory. First, we define all members of the family. Afterwards, we define exclusion constraints for invalid combinations. The DSL allows directed exclusions. Thus, both a conflicts b and b conflicts a have to be defined for undirected exclusions. Finally, past present combinations can be specified.

Afterwards, the Eclipse plugin will generate the respective ILP, triggers the ILP solver and will propagate back the valid solution:

Triggering ILP solving from the DSL.

Result of the ILP solving.

Finally, the implemented tooling can automatically add the newly computed solution to the program’s past presents rules to save the result within the program for the next year’s computation:

The present problem formulation with the newly added past present rules.

The source code for the respective Eclipse plugin is public available and can be obtained from http://code.google.com/p/code-candies/source/. Feel free to explore the tool with you own Christmas present problems.

For me the tool works just fine :)

[1] Wikipedia: Linear Programming. http://en.wikipedia.org/wiki/Linear_programming
[2] Sourceforge: LPSolve IDE. https://sourceforge.net/projects/lpsolve/files/lpsolve/
[3] EMFText. http://www.emftext.org/